Tabellen
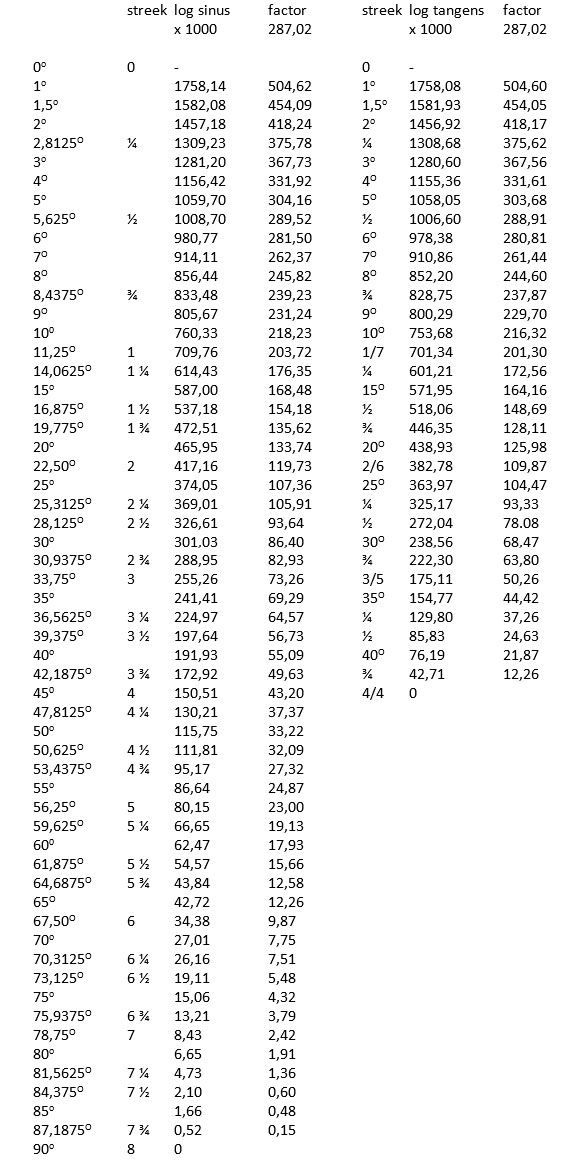
Tabel 1: Tabel wassende breedte, verkorting breedtecirkel en koorden mijlen t.o.v. breedtegraad
In de eerste helft van de 17e eeuw kon al gebruik worden gemaakt van de tafels van de wassende/vergrotende breedte op zeekaarten, zoals die o.a zijn vermeld in ‘De Seven boecken van de groote zeevaert’, 2e hoofdstuk, blz. 13, van Mr. Abraham de Graef, uitgegeven door Pieter Goos in 1658. In de tafels van de vergrotende breedte zijn de secanten samengevoegd en is 1o lengte in 600 tiende delen aangegeven. Door de getallen te delen door 600 vindt men het aantal vergrootte graden. In de 18e eeuw is bewezen dat de aarde bij de polen is afgeplat. De tafels van de wassende breedte zijn later gecorrigeerd (zie o.m. Handleiding tot de beschouwende en werkdadige stuurmanskunst, 2e deel, blz. 314, Mendoza, J.C. Pilaar, 1857). Ik heb gebruik gemaakt van de ‘oude tafels’. De nieuwe tafels zijn toegevoegd. (zie ook ‘the Works of James Ferguson’, blz. 303=304). Voor de maatvoering van een gunterscale zijn de verschillen beperkt.
Na de invoering van de integraalrekening kon de vergrootte breedte van een Mercatorkaart worden berekend met behulp van de volgende vergelijking:
VB = ½ ln (1 + sinφ) – ½ ln (1-sinφ); ⟶ VB in radialen, vermenigvuldigd met 180/π ⟶ VB in graden.
Eenvoudiger is de vergelijking: VB = ln tg(45o + ½φ), waarbij VB de vergrootte breedte in radialen en φ de breedtegraad.
Voorbeeld: voor φ = 60o ⟶VB = ln tg. 75o = 1,316957897 radialen; ⟶VB = 1,316957897 x 180o/π = 75,45613o. In tienden van boogminuten dus 45273,7 (in tabel 45274). Hierbij is geen rekening gehouden met de afplatting van de aarde.
Op gunterscale K, is de lengte ‘EP’ van 1o 2,9842 mm . Met deze lengte van 2,9842 mm stemmen de gemeten maten van de wassende breedte zowel op gunterschaal K als gunterschaal B overeen. Voor de berekening van de wassende breedte is voor de lengte van 1o 2,9842 mm aangehouden.
1: breedtegraad
2: wassende/vergrootte breedte in tienden van minuten
3: wassende breedte in mm: 1/600 x 2,9842 mm
4: lengte in mijlen ten opzichte van de breedtegraad (1o = 15 Duitse mijl)
5: lengte in mijlen ten opzichte van de breedtegraad (1o = 60 geografische mijl)
6: koorde (van de mijlen) ten opzichte van de breedtegraad (2 sin ½ φ) te vermenigvuldigen met de radius, dit is R x 2 sin ½ φ
Afstanden werden in mijlen aangegeven: in de Republiek in Duitse mijlen van 15 in een lengtegraad (op de equator), in Engeland 60 mijl en in Spanje en de Zuidelijke Nederlanden 17 ½ mijl.
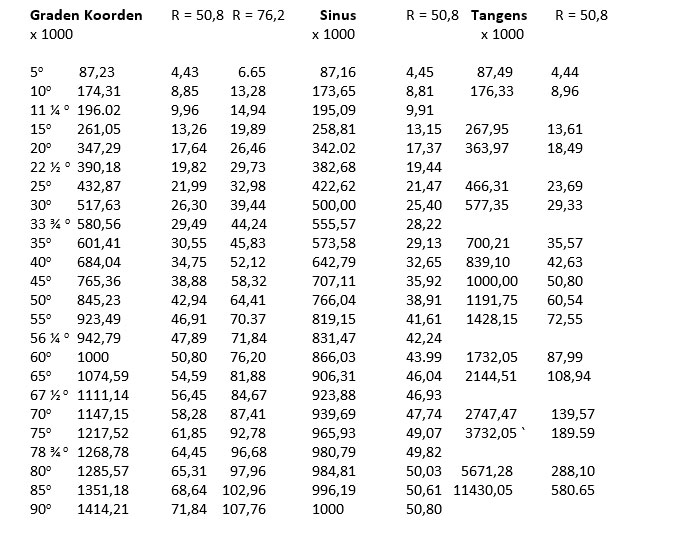
Zie ook tabel 2: graden koorden.
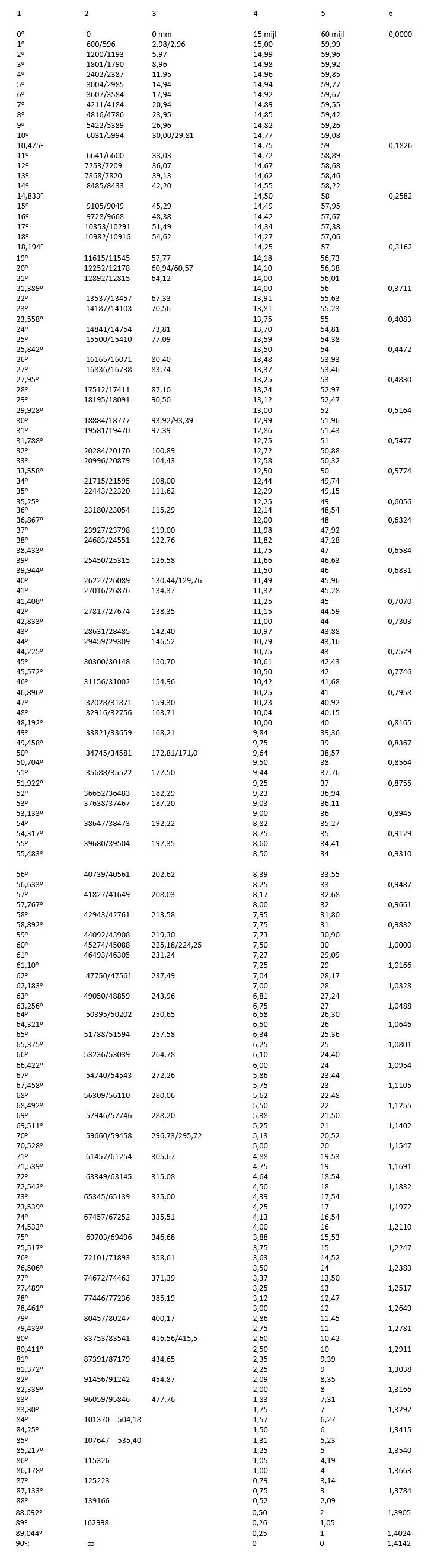
Tabel 2 Koorden, sinus en tangens
Koorden, sinus en tangens van de graden van 5o tot 90o, in een kwadrant met de radius 1000. De koorde van een hoek α = 2 sin ½ α bijv. koorde 60o= 2 sin 30o= 1.
Voor de koorden, sinus en tangenswaarden van alle graden zie ‘The works of James Ferguson F.R.S.’, 1823, blz. 287-290.
Tabel 3 Secans, log secans, STn (‘log sinus versus’), secant, sinus versus en log sinus versus
Sec2 α = 1 + tg2 α = 1 : cos2 α; sec α = √( 1 + tg2 α) = 1 : cos α
De sinus versus/versin of pijl α = 1 – cos α of 2 sin2 ½ α.
Log sinus versus (Vs), in plaats hiervan op gunterscale K:
STn α = 2 log secans ½ α (zie ‘the Works of James Ferguson’, blz. 299-301).
De secant (S) = secans α – 1000, waarbij R = 1000
Secans naar tafels ‘Complete mathematical and general navigationtables’, door Thomas Kerigan RN; sinus versus naar tafels Bernardus Joannes Douwes.
De schaalfactor/modulus is 287,02 mm

Tabel sec2 ½ α

Tabel 4 Log sinus en log tangens van de koorden en graden in mm