Gunterscales en pleinschalen

Pleinschaal Dierick Ruyter, Bellinckstraat, Middelburg, 1631

In ‘De platte ofte pleynschael’ wordt naast de toepassing van de pleinschaal in de zeevaart ook het gebruik beschreven voor het bepalen van de zondeclinatie in relatie met de poolshoogte, de variatie van het kompas en verticale en horizontale zonnewijzers. De pleinschaal in het boekje heb ik op groter formaat getekend.
In de zeevaart is deze pleinschaal te gebruiken voor gelijkgradige (platte) paskaarten. De methode van Dierick Ruyter is grafisch.
Hiertoe wordt een kwadrant getekend, zodat zonder te rekenen, de koers, verheid, veranderde breedte en veranderde lengte of afwijking, met een passer kunnen worden uitgezet of bepaald. In het kwadrant is de boogstraal (radius) gelijk aan de koorde van 60^o van de pleinschaal. Als lengte van de radius is aangehouden 100 mm. In de tijd van Dierick Ruijter zou dat ca. 4 duim zijn. 1 Duim Middelburgs/Bloois is 25 mm. De Amsterdams duim van 25,74 mm werd in Middelburg niet gebruikt. Op de betreffende boog kan de koorde van de streek of het aantal graden van de koers (in het voorbeeld 4 streken of 45^o) worden uitgezet en op de koerslijn de verheid (distantie). Op de noord- zuid richting worden de afgevaren breedte en bekomen breedte aangegeven, waarbij de veranderde breedte in graden en minuten wordt omgerekend in Duitse mijlen. Daarbij is 1^o gelijk aan 15 mijl en 4 minuten is 1 mijl. Voor het afpassen van de afwijking van de lengte, de veranderde breedte en de verheid wordt de mijlenschaal (regel 3) gebruikt. Voor een beperkt vaargebied, op geringe breedte en een koers die niet veel afwijkt van de richting noord- zuid wordt met deze vlakke driehoeksmeting geen grote fout gemaakt. Voor hoge breedte en groot vaargebied is de methode van vlakke driehoeksmeting onbruikbaar omdat de afstand tussen de lengtegraden (meridianen) verandert met de breedtegraad. Op een gelijkgradige paskaart is een koers buiten de richtingen noord- zuid en oost- west geen rechte lijn maar een spiraal richting pool, een loxodroom; de streek en veranderde lengte (afwijking) die op de platte kaart worden uitgezet zijn dus niet juist.
In het voorbeeld is de afwijking op de pleinschaal door afpasseren te bepalen op 52,5 mijl, dit is 3,5^o. In plaats van de grafische methode kan volgens de platte driehoeksberekening van een rechthoekige driehoek, waarvan de 2 zijden bekend zijn of een zijde en een hoek, de onbekende hoek of zijde worden berekend. Als de veranderde breedte en de verheid of koers(hoek) bekend zijn: veranderde lengte = veranderde breedte x tg koers 45^o = 52,5 x 1 = 52,5 mijl of 3,5^o.

Een nauwkeuriger manier om het lengteverschil of afwijking grafisch te bepalen is volgens Dierick Ruyter de volgende: op het kwadrant midden tussen de veranderde breedte (3,5^o) de middelbreedte in graden bepalen en uitzetten in mijlen. Deze middelbreedte in graden (49^o) afpassen op de koordenschaal regel 2; hieruit volgt de lengte van deze koorde (8,29386 cm^*1) en deze lengte afpassen op de linie van regel 5 (vanaf 15). Hieruit volgt 9,84 mijl^*2 om een graad in lengte op de middelbreedte te veranderen. Dit aantal mijlen als voetpunt van de passer op de linie van regel 4 plaatsen en het andere voetpunt naar rechts op 1 afpassen. Deze passeropening is lengte b/log b (10,7574 cm^*3).

*1 2 sin ½ x 49^o = 0,829386
*2 cos 49^o x 15 mijl = 9,841 mijl
*3 log 9,84 x 10,833 cm = 10,7574 cm

Vervolgens op het kwadrant de afwijking (lengteverschil) behorend bij het breedteverschil afpassen en op de mijlenschaal regel 3 het aantal mijlen bepalen, dit is 52,5 mijl. Op de linie van regel 4 de afwijking (lengteverschil) in mijlen afzetten (log a). Op dit voetpunt van 52,5 (dit is vanaf 1: log 52,5 x 10,833 = 18,6350 cm) met de passer de lengte b (10,7574 cm) in de richting van 1 uitzetten. Dit punt ligt op ca. 5,3 van regel 4 en betreft het lengteverschil in graden (zie tekening pleinschaal). Dit punt kan ook worden berekend:
log a : log b = log a – log b, ⟶ 18,6350 – 10,7574 = 7,8776 cm vanaf 1 gemeten. De log van het lengteverschil is 7,8776 : 10,833 = 0,7272. Het lengteverschil (ten opzichte van de afgevaren plaats) is hierbij ca. 5,335^o. Het Lengteverschil in graden is dus groter dan volgens de eerder vermelde vlakke driehoeksmeting (3,5^o).
De onderstreepte maten zijn berekend.

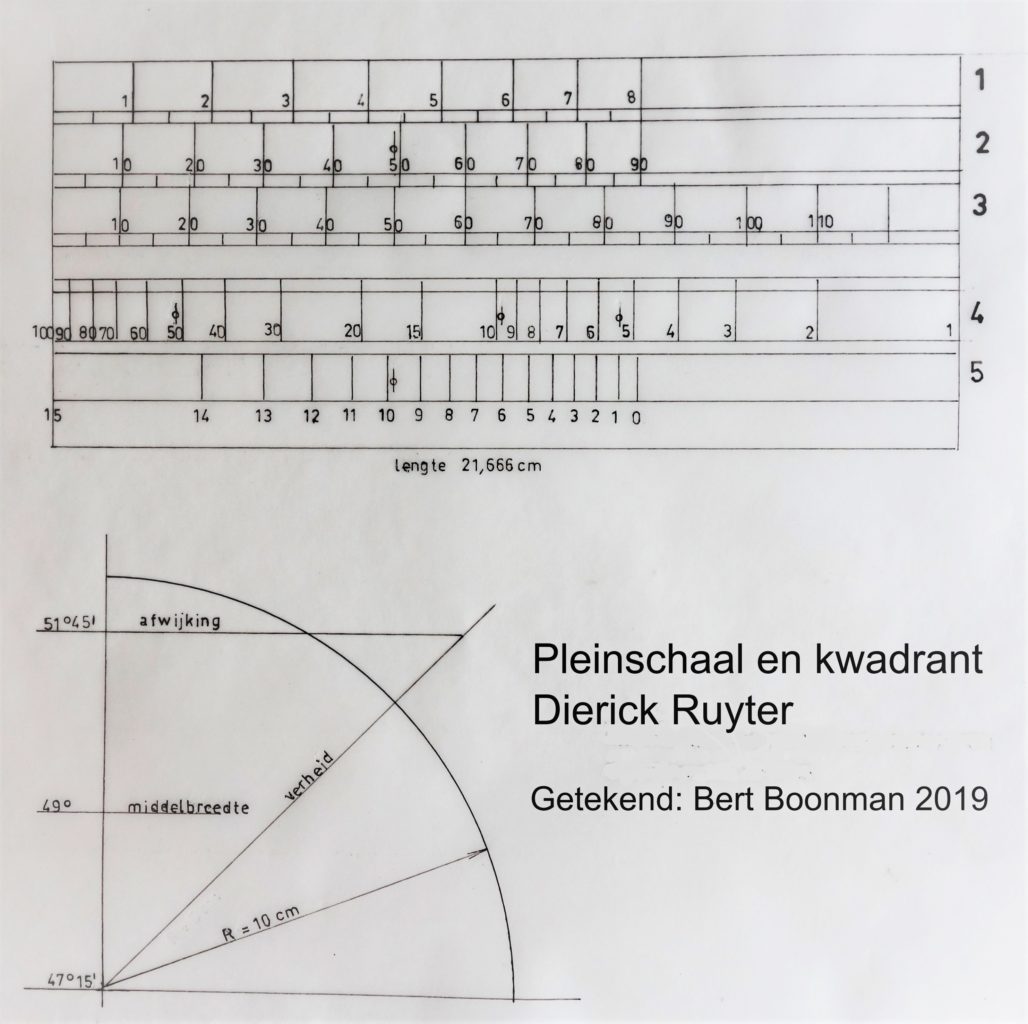
Regels op de pleinschaal: voorzijde
Regel 1: linie koorden streken of rumben 1-8. Om de koers op de kaart over te brengen. Verdeling in halve streken. Op andere pleinschalen vaak verdeeld in kwart streken. De lengte is resp. streek 1: 19,6; streek 2: 39,0; streek 3: 58,1; streek 4: 76,5; streek 5: 94,3; streek 6: 111,1; streek 7: 126,9; streek 8: 141,4 mm.
Regel 2: linie koorden graden 0-90; de lengte is resp. 10^o: 17,4; 20^o: 34,7; 30^o: 51,8; 40^o: 68,4; 50^o: 84,5; 60^o: 100; 70^o : 114,7; 80^o: 128,6; 90^o: 141,4 mm. De koorde van 60^o is 100 mm. Dit is de radius.
Regel 3: linie mijlen of gelijke delen 0-110-130. Op de pleinschaal van Ruyter komt 60 mijl ongeveer overeen met de radius of de koorde van 60^o. Dit is aangehouden voor de getekende pleinschaal. 130 mijl komt hierbij overeen met 216,66 mm. Ruijter heeft echter met duimen gewerkt; mogelijk heeft hij voor de gelijke delen 1 Middelburgse duim aangehouden voor 15 mijl, dus 2/3 duim voor 10 mijl en 8 en 2/3 duim voor 130 mijl. De lengte hiervan is 216,66 mm, zoals hiervoor is vermeld. Met deze lengte is het een handzame pleinschaal.

Regels op de pleinschaal: achterzijde
Regel 4: linie lengteverschil volgens Ruijter, in 2 gelijke delen van links (100) naar rechts (10) en van (10) tot (1). De totale lengte van de linie is gelijk aan de linie van regel 3 van de gelijke delen, die 216,66 mm is. De schaal is logaritmisch. Log 100 = 2 komt overeen met 216,66 mm. De schaalfactor is 216,66 : 2 = 108,33. De lengte van Log 1 = 0; log 2: 32,61; log 3: 51,69; log 4: 65,22; log 5: 75,72; log 6: 84,30; log 7: 91,55; log 8: 97,83; log 9: 103,38; log 10: 108,33; log 11: 112,82; log 12: 116,9; log 13: 120,67; log 14: 124,16; log 15: 127,41; log 20: 140,94; log 30: 160,02; log 40: 173,55; log 50: 184,05; log 60: 192,63; log 70: 199,88; log 80: 206,17; log 90: 211,71; log 100: 216,66 mm.
Ruyter vermeldt niet dat regel 4 een logaritmische schaal betreft. Logaritmische tabellen van Briggs zijn vanaf ca. 1630 in Nederland bekend geworden en later in Nederland gedrukt.
De pleinschaal van Ruyter is waarschijnlijk het eerste voorbeeld van een logaritmische schaal op een Nederlandse pleinschaal.
Regel 5: linie lengteverschil in mijlen tussen de meridianen op verschillende breedtegraden. Op de evenaar is 1 graad lengteverschil 15 mijl, op de polen 0 mijl. Daartussen is het lengteverschil op de breedtegraad φ : cos φ x 15 mijl. Op de linie zijn de mijlen aangegeven van 15 tot 0. Het betreft dus Duitse mijlen van 15 in een graad, zoals gebruikelijk in de Republiek; de tekening is dus geen Engelse kopie, want daar werd 60 mijl in een graad gerekend.
Hiervan is de bijbehorende breedtegraad berekend en vervolgens de koorde. Gemeten van links (15) is van 15 tot 0 mijl de lengte van de koorde resp. 15 mijl: 0; 14 mijl: 36,5; 13 mijl: 51,65; 12 mijl: 63,24; 11 mijl: 73,03; 10 mijl: 81,65; 9 mijl: 89,45; 8 mijl: 96,60; 7 mijl: 103,28; 6 mijl: 109,54; 5 mijl: 115,40; 4 mijl: 121,11; 3 mijl: 126,50; 2 mijl: 131,65; 1 mijl: 136,63; 0 mijl: 141,14 mm.

Afpasseren was inzichtelijk en had de voorkeur boven lastig rekenen.
In de loop van de 17e eeuw zijn tafels van de kromstreken beschikbaar gekomen. Per streek is hierop aangegeven voor verheden vanaf 1 mijl en oplopend, de bijbehorende breedte en lengte in graden en minuten, tot ruim 70^o breedte.
In plaats van de gelijkgradige platte paskaarten om de vaarroute uit te zetten, is steeds meer gebruik gemaakt van zeekaarten met vergrotende breedte. Hierop kan de koers als rechte lijn worden uitgezet. Ook van de vergrotende of wassende breedte zijn in de 17e eeuw tafels beschikbaar gekomen.

Pleinschaal Symon vande Moolen

Symon vande Moolen vermeldt in ‘Klaare beschrijvingh over het maken en gebruyk der nieuwe pleyn-schaal’, in 1699, dat de pleinschaal werd gebruikt in de ‘astromia, geometria, gnomonica (zonnewijzertechniek), fortificatie, bosschieterij en in het bijzonder in de navigatie.’ Scheepvaartmuseum Amsterdam, inv. nr.  S. 4793; MK-0605.

De pleinschaal is een houten plankje van ongeveer 1 voet lang en 1 ½ duim breed en is verdeeld in 11 gelijke delen en aan elk einde is een deel  ‘van ontrent een duim’ gedeeld in 10 delen en door de schuine strepen in 100 gelijke delen om roeden, voeten, duimen, mijlen enz. af te passen en aan  het andere eind in 60 gelijke delen om minuten af te afpassen.

De afbeelding van de pleinschaal is vanwege de lengte 2 x gevouwen. De lengte van de schaalverdeling is ca. 250 mm, de breedte is ca. 62 mm. De opmetingen zijn op 0,5 mm nauwkeurig. Vermoedelijk is de afbeelding in het boekje op ware grootte afgedrukt. Vanwege de vouwen en de mogelijke krimp van het papier zijn de opmetingen en daarvan afgeleide berekeningen van een beperkte nauwkeurigheid.

Maatverdeling

Bovenste regel: de gelijke delen/vakken. De verdeling is in 22 gelijke vakken, waarvan 13 genummerd. Aan weerszijden zijn enkele vakken met transversalen, links in 100ste delen en rechts in 60ste graden (minuten). De verdeling van de gelijke vakken is te gebruiken om de koers en verheid (afstand) af te passen of om mijlen, graden, roeden of voeten grafisch te bepalen.
De lengte van 1 vak ca. is 250 : 22 = ca. 11,36 mm is. De lengte van de 5 vakken aan de uiteinden is ca. 57 mm, waarbij de lengte van 1 vak 11,4 mm is. Over 10 vakken in het middendeel is als lengte gemeten 113,5 mm, waarbij de lengte van 1 vak 11,35 mm is. Deze lengte is hierna aangehouden. De nummering van de vakken is van 1 tot 13 en in tegengestelde richting van 13 tot 1. De verdeling van de pleinschaal over de gehele lengte is in 22 vakken, in plaats van de door Vande Moolen genoemde 11 delen. De delen zoals Vande Moolen die noemt, van ‘ontrent een duim’, zijn dus ca. 22,7 mm lang. Dit is te klein voor de lengte van een duim (Rijnlands 26,16 mm; Amsterdams 25,74 mm) De maat van de gelijke vakken is vermoedelijk willekeurig.

Regel 1 en regel 2: de vergrotende/wassende breedte is onder de verdeling van de gelijke vakken aangegeven. Regel 1 van 60^o tot 83^o, regel 2 van 0^o tot 64^o.
Vande Moolen beschrijft een grafische manier om de vergrotende breedte op een pleinschaal over te brengen. Hierbij wordt de gekozen lengte van een graad (op de equator) afgepast op de halve middellijn/radius van een ‘vierendeel rond’, zoals Vander Moolen een kwartcirkel of kwadrant met een bepaalde radius noemt. De lengte van de lijn die een hoek maakt met de verticaal vanuit een graad op de halve middellijn is de snijlijn/secans of vergrotende breedte van de hoek. In plaats van deze grafische methode is vermoedelijk gebruik gemaakt van de tafels van de wassende breedte. Voor de pleinschaal kan de wassende breedte in 10den van minuten worden omgerekend in mm’ s naar de lengte van 2,91857 mm per graad (zie regel 3). Voorbeeld: wassende breedte 35^o is 22443 tienden van minuten, dit is 22443 : 600 = 37,405^o De lengte op de pleinschaal is 37,405 x 2,91857 mm = 109,17 mm (zie tabel 1)

Regel 3: betreft de lengteschaal van de graden op de equator van 0^o tot 70^o . De lengte van het eerste vak van 10 graden is in 10 delen verdeeld van elk 1^o, zodat in graden of delen ervan kan worden afgepast. Volgens Vande Moolen is afpassen in 3e, 4e of 5e delen van een graad mogelijk.
Op de pleinschaal komt de lengte van 18 vakken van de maatverdeling van de gelijke vakken overeen met 70 graden lengte op de equator. De lengte van 1 graad op de pleinschaal (of 15 Duitse mijl) is 18 x 11,35 mm : 70 = 2,91857 mm. Een vak van 11,35 mm komt hierbij overeen met 58,3333 Duitse mijl.
Conclusie : Er is geen verband tussen de lengte van de graden en de lengte van de gelijke vakken.

Regel 4: de koorden van de uren van 0 tot 6 uren, elk uur 15^o, met een verdeling in kwart uren.

Regel 5: de koorden van de streken van 0 tot 8 streken, elke streek 11 ¼^o met een verdeling in kwart streken.

Regel 6: de koorden van 0^o tot 90^o, met een verdeling in graden.

Regel 7: de hoekmaten (sinuswaarde) van 0^o tot 90^o.

Regel 8: de hoekmaten op streken van 0 tot 8, met een verdeling in kwart streken.

Regel 9: de hoekmaten op uren, met een verdeling in kwart uren.

Regel 4 tot en met regel 9 hebben betrekking op de koordenschaal met een grote radius. De opgemeten lengte van deze radius is 87 mm en van de uren, streken, en koorden 123 mm. De lengte van de uren- streken- en koordenschaal moet zijn √2 x 87 mm of 123,04 mm. De radius komt hierbij overeen met ca. 447,15 Duitse mijl.
De lengte van de radius op de tekening van de pleinschaal valt exact samen met 30 graden op de lengteschaal, waarbij de radius 30 x 2,91857 mm = 87,5571 mm is (in plaats van 87 mm). Hierbij wordt de lengte van de uren- streken- en koordenschaal √2 x 87,5571 mm = 123,8 mm. De radius van 87,5571 mm komt dan overeen met 30 graden of 450 Duitse mijl. In dat geval is er dus een verband tussen de radius en de schaal van de kaart (de lengtegraad op de equator).

Naast deze grote radius van de koordenschaal zijn op de pleinschaal nog 2 verschillende koordenschalen aangegeven, een met een middelbare en een met een kleine radius.
De middelbare radius is 34,5 mm en de lengte van de daarbij behorende uren- streken- en koordenschaal 49 mm. Hierbij is de radius ca. 177 Duitse mijl. Indien wordt uitgegaan van een radius van 35 mm komt de radius overeen met ca. 180 Duitse mijl.
De koordenschaal met de kleine radius is met transversalen van 0^o tot 90^o en een strekenschaal van 8 streken aangebracht.
De radius van de kleine koordenschaal is 27 mm : √2, dit is 19,09 mm . Hierbij is de radius ca. 98 Duitse mijl. Indien uitgegaan wordt van een radius van 19,5 mm is deze ca. 100 Duitse mijl.
De vermoedelijke verhouding tussen de grote, middelbare en kleine koordenschaal is 450 : 180 : 100 of 7,5 : 3,0 : 1,67. Op andere Nederlandse pleinschalen komt een verhouding voor van 7,5 op 3. De verhoudingen van de radii van de grote en middelbare koordenschaal stemmen hiermee overeen.
Bij de berekening van de hoekwaarden en koorden is uitgegaan van de vermoedelijke lengte van de radii van (afgerond 87,56) mm, 35 mm en 19,5 mm (zie tabel 2).
Waarschijnlijk bestaat een verband tussen de verschillende radii en de schaal van groot en klein bestek zeekaarten (overzeilers). Tussen de lengte van de gelijke vakken en de lengte van de radii is geen verband gevonden.

Pleinschaal Abraham de Graef

In ‘De seven boecken van de groote zeevaert, zevende boek’, eerste hoofdstuk, van Mr. Abraham de Graef, uitgegeven door Pieter Goos in 1658 is een voorbeeld van een pleinschaal opgenomen. (Scheepvaartmuseum  S.4793; 038) Abraham de Graef vermeldt dat voor het maken van een pleinschaal een klein houtje van omtrent een voet lang en anderhalve duim breed gebruikt kan worden. Het is niet bekend of de afbeelding op ware grootte is; de opgemeten lengte in het boek is ca. 227 mm en is verdeeld in 2 gelijke delen van 113,5 mm.

Maatverdeling

A-B: de 8 kompasstreken of romben/rumben, van links (8) naar rechts (1). De kompasstreken zijn in vieren onderverdeeld. De getekende lengte is ca. 113,5 mm.

C-D: de  koorden van de hoeken van links (90^o) naar rechts (0^o), verdeeld in tientallen graden en onderverdeeld in graden; de getekende lengte is evenals van de romben ca. 113,5 mm. Hierbij is de radius 113,5 mm :  = ca. 80 mm (3 Amsterdamse duim zou zijn 3 x 25,74 mm = 77,22 mm). Aangehouden is een radius van 80 mm. De lengte van een koorde van hoek α is 2 x sin ½ α x radius. Voor α = 30 graden is dit ca. 0,518 x 80 mm = 41,4 mm. De koorden van de hoeken en streken zijn vermeld in tabel 2.

E-F: de longitude van de lengtegraden ten opzichte van de breedtegraden in Duitse mijlen van 15 in een graad. Genummerd van links: 0 mijl (90^o) naar rechts: 15 mijl (equator: 0^o). Hiermee wordt het aantal mijlen aangegeven om op een bepaalde breedte φ, in oostelijke of westelijke richting een verschil van 1 lengtegraad  te bereiken. Op een breedte φ is dit cos φ x 15 mijl. Op 60^o breedte is dit 0,5 x 15 = 7,5 mijl  (tabel 1, kolom 4).

Voor 1 Duitse mijl (15 Duitse mijl in 1 graad) werd in de 17^e eeuw 1900 Rijnlandse roeden aangehouden, dit komt overeen met 7158 m. De lengte van 1 Duitse mijl is later op basis van de aardomtrek van 40.000 km vastgesteld op 7407 m.

G-H: de linie van de gelijke delen (mijlen) van links (100) tot rechts (0) met een verdeling in tientallen en een onderverdeling in mijlen. De opgemeten lengte van 100 mijl is ca. 227 mm, zodat 10 mijl 22,7 mm is. Er is geen verband met de Amsterdamse voet/duim.

I-K : de numerieke logaritmische schaalverdeling van links (100) naar rechts (10) en van 10 tot 1, over een totale lengte van totaal 227 mm, waarvan log 10 het midden is. De lengte van log 1 tot log 10 is 113,5 mm. Deze lengte komt overeen met log 10. Omdat log 10 = 1, is de schaalfactor 113,5. Log 1 is 0;  log 2 is 0,30103 x 113,5 mm = 34,17 mm; log 3: 54,15 mm; log 4: 68,33 mm; log 5: 79,33 mm; log 6: 88,32 mm; log 7: 95,92 mm; log 8: 102,50 mm; log 9: 108,31 mm. De onderstreepte maten zijn berekend.

De functie en het gebruik van deze schaalverdeling is overeenkomstig met die van de pleinschaal van Dierick Ruyter. De maatvoering is in verhouding met de lengte van 227 mm (de Graef) en 216,66 mm (Ruyter). De lengte van bijv. log 5 op de pleinschaal van Ruyter is 75,719 mm. Op de pleinschaal van De Graef dus 227/216,66  x 75,719 = 79,333 mm.

Voor de koorden en het lengteverschil in mijlen is de verhouding van de radii (80 mm De Graef, 100 mm Ruyter) bepalend. De koorde van 30 ^o is op de pleinschaal van Ruyter 51,8 mm. Op de pleinschaal van De Graef dus 80/100 x 51,8 mm = 41,44 mm.
Conclusie: Als de maatvoering van een pleinschaal correct is berekend, kan met de verhoudingen van de lengte en van de radii, de maatvoering van andere pleinschalen direct worden bepaald of gecontroleerd.  

De verhoudingen in de maatvoering van de tekening  in het boek zijn correct. De hoekwaarde (sinus) is op de afbeelding niet aangegeven.

Andere pleinschalen

De maatvoering van de pleinschaal van ’t  Vliegend Hert’ (Maritiem Museum Vlissingen) en van de pleinschaal M 66-7 in het Zeeuws Museum zijn op een soortgelijke manier beschreven en voor belangstellenden te raadplegen. De radius van de koordenschaal ’t Vliegend Hert is 47 mm. De 3 radii van de koordenschalen van de pleinschaal M 66-7 zijn 75, 30 en 22,5 mm.