Gunterscales en pleinschalen

De sector is een latere versie van de gewone tweebenige timmermansmeetlat van 12 inch per been (‘A decade of accessions’, door J.A. Benett, 1992, Whipple Museum, Cambridge).
Sector (Engels) wordt in het Frans compas de proportion (Frans) genoemd en heet proportionaalpasser in het Nederlands.

De sector bestaat uit 2 benen van gelijke lengte, die scharnierend verbonden zijn. De functies van een sector zijn vergelijkbaar met die van een gunterscale. Vanwege de beperkte lengte is een Meriodinal scale voor Mercator kaarten niet aanwezig. Het gebruik vereist een scherpe blik.     

Principe sector

Indien de benen gedeeltelijk worden geopend, vormen deze vanuit het centrum een gelijkvormige driehoeken, met  bepaalde verhoudingen van de lengte van de zijden. Uit deze verhouding kunnen trigonometrische vraagstukken grafisch worden opgelost. Hierbij wordt de afstand vanuit het centrum ‘lateral distance’ genoemd en de afstand tussen de benen van overeenkomende schalen van koorden, sinussen, tangenten enz.  ‘transverse distance’.  Met behulp van een sector en passers kunnen vrijwel alle vlakke-  en boldriehoeksberekeningen grafisch worden uitgevoerd.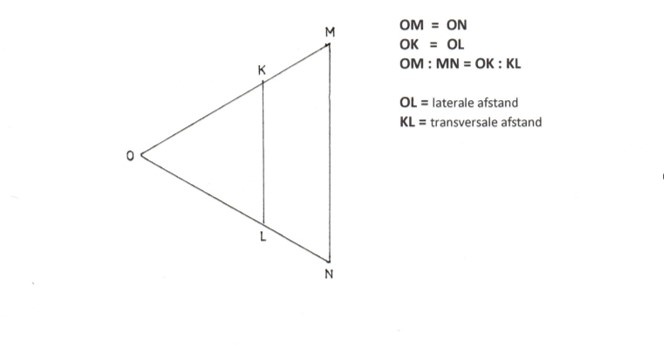

Voorzijde (met opschrift T &T Blunt; (centrum scharnier onder)

Ivoor met ronde messing verbinding.
Lengte 6 inch per been; totale lengte 12 inch. 
Gemerkt T &T Blunt, London; datering 1801-1822
Boven (uitgeklapt) van rechts naar links 0 -12 inch, elke inch in 10 delen.
Totale lengte ca. 304 mm, dit is 25,33 mm/inch (1 inch = 25,4 mm).

Op elk been:
L:  linie van ‘lines’ van centrum naar eind 0-10; 10 gelijke vakken, elk vak verdeeld in 10 delen; totale lengte 148 mm of 5,827 inch. Deze schaallengte  komt overeen met de radius R. Gebruikelijk is R = ca. 5 ¾  inch of 146 mm. Op 10 voetpunt.

s:  linie van ‘secants’ van centrum naar eind 20 ^o -75 ^o. 0 ^o  op eindstreepje, ca. 37 mm uit centrum. Gebruikelijk is een kwart van de lengte van de radius, dus ¼ x 5 ¾  inch of ca. 36,5 mm. Uitgegaan is van 37 mm volgens de opmetingen. Verschil sec 20 ^o (1,06418) en sec 75 ^o(3,86370) is 2,79952. De lengte tussen sec 20 ^o en sec 75 ^o is ca. 103,7 mm, zodat R = 103,7 : 2,79952 = 37,04 mm

Idem verschil tussen sec. 20 ^o (1,06418) en sec. 60^o (2,00000) is 0,93582. De lengte tussen sec 20 ^o en 60 ^o is ca. 34,7 mm, zodat R = 34,7 :  0,93582 = 37,1 mm.

C: linie van ‘chords’/koorden van centrum naar eind van 0 ^o – 60 ^o over 148 mm. Koorde 60 ^o = 1 zodat R = 148 mm. Op 60^o voetpunt.

POL: linie van ‘polygons’/polygonen, langs de binnenzijde , genummerd 4 tot 12.  De lengte van een zijde van een polygoon is de koorde van de hoek of 2 x de sinus van de halve hoek vermenigvuldgd met de straal (R).

Voorbeeld:  koorde 10 hoek (10) is 2 sin 18 ^o R = 0,61803 R. R is de straal van de omgeschreven cirkel.

De koorde (zijde) van de vierhoek (4) is 2 sin 45 ^o. R  = 1,41421 R en vormt de basis van de gelijkbenige driehoek met de top in het centrum. De beenlengte is 148 mm. Hieruit kan de afstand a tot het centrum worden berekend.

Voor de 10 hoek:  a : 0,61803 = 148 : 1,41421, zodat  a = 64,68 mm en t.o.v. de basis 148 – 64,68 = 83,32 mm.  De gemeten afstanden in mm tot het voetpunt zijn (4): 0, (5):24,9/25, (6): 43,3/43,3, (7): 57,2/57,2, (8):68/67,9, (9):76,3/76,4, (10): 83,3/83,3, (11): 89/89, (12): 94/93,8. De berekende waarden (afgerond) zijn onderstreept.

Voor bijv. 360.000 veelhoeken (1/1000 ^o) is de koorde 2 x sin 0,0005 R. Vermenigvuldigd met het aantal veelhoeken (360.000) ⟶ de totale omtrek 6,283185307R; gedeeld door 2 R is 3,141592654, dit is bij benadering het ‘magische’ getal π.     

Zie figuur koorden (zijden) polygonen 1-12; R = 148 mm.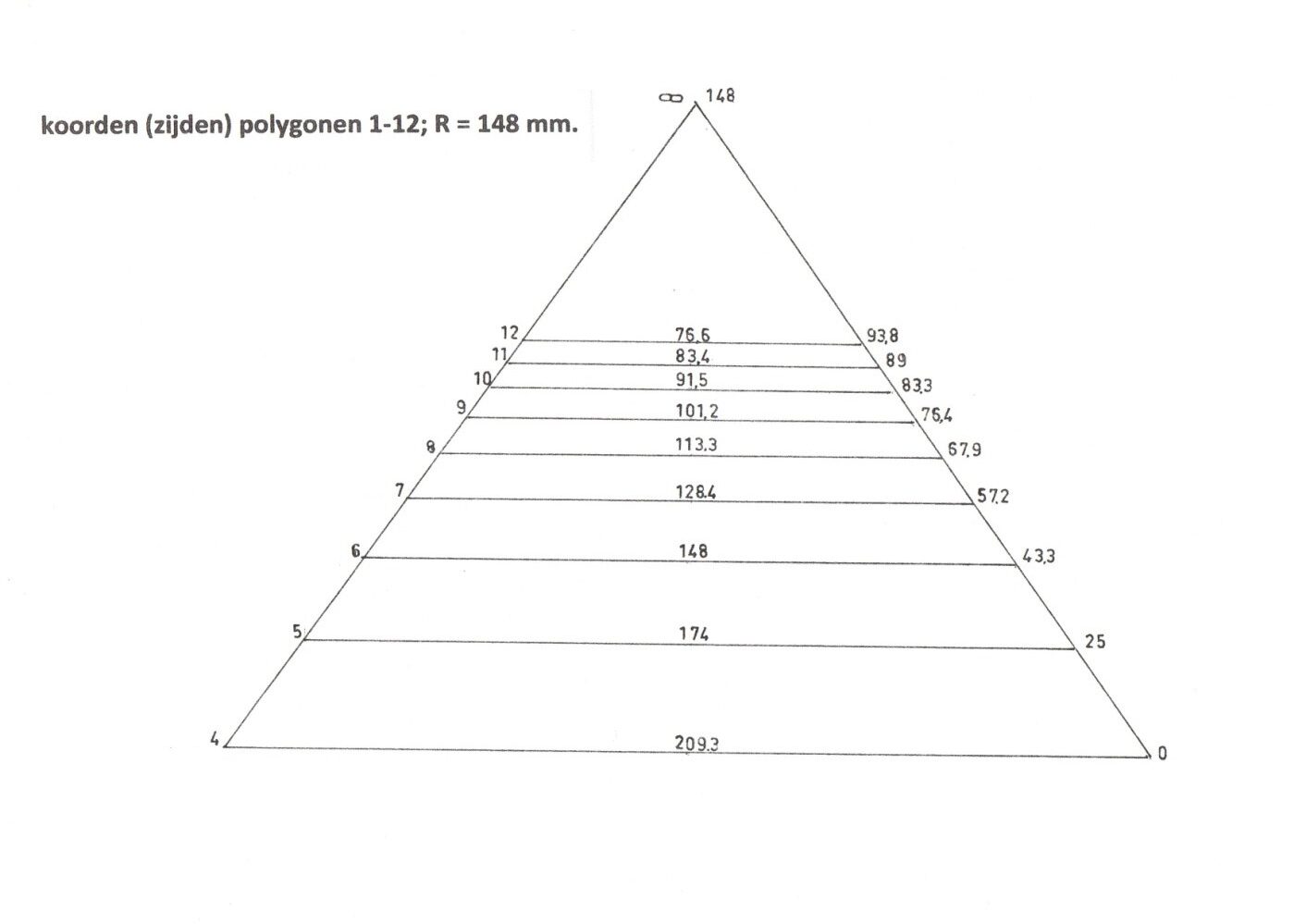
Achterzijde (centrum scharnier onder)

Op elk been: S: linie van  ‘sines’ van centrum 0 naar eind 90 over 148 mm. Sin 90 ^o = 1 zodat R = 148 mm. Voetpunt op 90 ^o.  
T: linie van ‘tangents’/ tangenten van centrum 0 ^o naar eind 45 ^o . lengte 148 mm. Tg 45= 1, zodat R = 148 mm. Voetpunt op 45 ^o.

t:  linie van ‘tangents’/tangenten van 45 ^o (op 37 mm van centrum) naar 75 ^o (op ca. 10 mm van eind (gebruikelijk is ¼  van de totale lengte, dit is ca. 37 mm). Lengte tussen tg 45 ^o (1,000) en tg 75 ^o (3,73205) is 101,5 mm, zodat  R = 101,5 : 7325 mm =  37,15 mm. De gemeten lengte wijkt niet veel af van R= ¼ x 5 ¾  inch (ca. 36,5 mm)

Uitgeklapt:

*n: ‘Gunter’ linie doorlopend  van log 1 tot log 10  en van log 1 (10) tot log 10 (100).  Gemeten lengte 126,5 mm; aangehouden 127 mm (5 inch).  Voetpunt op log 10 (100). De voetpunten van de logschalen zijn ruim 40 mm uit de kant aangebracht.  

*t: linie log tangens, doorlopend van de kant 2 ^o via centrum naar 45 ^o-. Lengte ca. 184,5 mm komt overeen met verschil log tangens 2 ^o (1,4569) en log tangens 45^o (0) is 1,4569. De schaalfactor is 184,5 : 1,4569 = 126,6. Aangehouden 127. Voetpunt op 45^o.

*S:  linie log sin doorlopend van de kant 1 ^o via centrum naar 90 ^o. Lengte 222,5 253 mm komt overeen met verschil log sin 1 ^o (1,7581) en log sin 90^o (0) is 1,7581. De schaalfactor is 222,5 : 1,7581 = 126,6. Aangehouden 127. Voetpunt op 90 ^o.

Zijkant
Doorlopende voetverdeling 0- 100 voet, onderverdeling in 10 tallen voeten, schaal 1: 100.

 Literatuur
‘Description and use of the sector’, door Edmund Weaver,1624 ‘Treatise on Gunter’s scale’, door Georges Curtis, 1804
‘The Construction and principal uses of mathematical instruments’, door H. Bron, 1758